Units and Measurement Class 11 Notes For Physics Chapter 2
standard units of measurement, basic units of measurement, all units of measurement, si units of measurement, units of land measurement, units of weight measurement, units of measurement conversion, different units of measurement, units of measurement of land, fundamental units of measurement, physics units of measurement, non standard units of measurement, units of measurement in physics, units of area measurement, conversion of units of measurement, international units of measurement, differen, units and measurement 11 notes, class 11 physics notes, units and measurement class 11, units and measurement class 11 notes, class 11 units and measurement, note physics, physics notes, units and measurement, class 11 cphysics chapter 2 notes, 11th standard physics notes, 11th std physics
Units of Measurement Physics Class 11 Download in pdf
Measurement of physical quantities
Physics is a quantitative science, based on measurement of physical quantities.Certain physical quantities have been chosen as fundamental or base quantities. The fundamental quantities that are chosen are Length, Mass, Time, electric current, thermodynamic temperature, amount of substance, and luminous intensity.
Base quantity and Fundamental Units
Each base quantity is defined in terms of a certain basic arbitrarily chosenbut properly standardised reference standard called unit (such as metre,kilogram,second,ampere,kelvin,mole,and candela.The units for the fundamental base quantities are called fundamental or base units and two supplementary units in relation to quantities plane angle and solid angle radian, Ste radian..
| S.No. | Fundamental Quantities | Fundamental Units | Symbol |
| 1. | Length | metre | m |
| 2. | Mass | kilogram | kg |
| 3. | Time | second | S |
| 4. | Temperature | kelvin | kg |
| 5 | Electric current | ampere | A |
| 6 | Luminous intensity | candela | cd |
| 7 | Amount of substance | mole | mol |
Derived units
Other physical quantities derived from the base quantities can be expressed as a combination of the base units and are called derived units.A complete set of units both fundamental and derived units are called a system of units. Example :- volume, density etc
International System of units
*The International System of units based on seven base unitsis at present internationally acceptedunit system and is widely used throughout the world. In computing any physical quantity the units for derived quantities involved in the relationships are treated as though they were algebraic quantities till the desired units are obtained
- CGS System In this system, the unit of length is centimetre, the unit of mass is gram and the unit of time is second.
- FPS System In this system, the unit of length is foot, the unit of mass is pound and the unit of time is second.
- MKS System In this system, the unit of length is metre, the unit of mass is kilogram and the unit of time is second.
- SI System This system contain seven fundamental units and two supplementary fundamental units. The SI units are used in all physical measurements, for both the base quantitiesand the derived quantities obtained from them. Certain derived units are expressed by means of SI units of special names such as joule, newton, watt etc.
* In computing any physical quantity the units for derived quantities involved in the relationships are treated as though they were algebraic quantities till the desired units are obtained
* In SI system that is System Internationale d’ Units there are 7 base units’ andtwo supplementary units.
| S.No. | Supplementary Fundamental Quantities | Supplementary Unit | Symbol |
| 1 | Plane angle | radian | rad |
| 2 | Solid angle | steradian | Sr |
* Direct and indirect methods can be used for the measurement of physical quantities. In measured quantities while expressing theresult, the accuracy and precision of measuring instrumentsalong with errors in measurement should be taken into account.
* In measured and computed quantitiesproper significant figures only should be retained.
Use of Dimensional analysis
* The dimensions of base quantities and combination of these dimensions describe the nature of physical quantities .Dimensional analysis can be used to check the dimensional consistency of equations, deducing relations among physical quantities etc. A dimensionally consistent equation need not be actually an exact equation, but a dimensionally wrong or inconsistent equation must be wrong.
Error
The uncertainty in the measurement of a physical quantity is called an error.
The errors in measurement can be classified as (i) Systematic errors and (ii) Random errors
SYSTEMATIC ERRORS:
These are the errors that tend to be either positive or negative.Sources of systematic errors are
(i) Instrumental errors
(ii) Imperfection in experimental technique or procedure
(iii) Personal errors
RANDOM ERRORS :
Those errors which occur irregularly .These errors arise due to unpredictable fluctuations in experimental conditions
Least count error
Least count error is the error associated with the resolution of the instrument.
Absolute error
The magnitude of the difference between the individual measurement and the true value of the quantity is called the absolute error of the measurement.

Mean Absolute Error
The arithmetic mean of all the absolute errors is taken as the final or mean absolute error of the value of the physical quantity a. It is represented by Δa mean
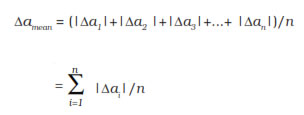
Relative error - it is the ratio of the mean absolute error to the true value.
Relative error = Δa mean/ a mean
Percentage Error : When the relative error is expressed in per cent, it is called the percentage error (δa).
COMBINATION OF ERRORS
ERROR OF A SUM OR A DIFFERENCE
When two quantities are added or subtracted, the absolute error in the final result is thesums of the absolute errors in the individual quantities.
IF Z=A+ B then the max possible error in Z, ∆Z =∆A + ∆B
IF Z=A- B then the max possible error in Z, ∆Z =∆A + ∆B
ERROR OF A PRODUCT OR A QUOTIENT
When two quantities are multiplied or divided the relative error is the sum of the relative errors in the multipliers
Suppose Z= A*B or Z=A/B then the max relative error in ‘Z’ = ∆Z/Z= (∆A/A) + (∆B/B)
ERROR IN CASE OF A QUANTITY RAISED TO A POWER
The relative error in a physical quantity raised to the power k is the k times the relative
error in the individual quantity.
Suppose Z = Ak
then ∆Z/Z = K (∆A/A)
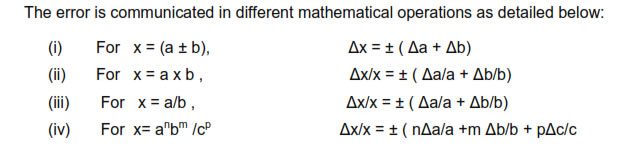
Significant figures: -
The significant figures are normally those digits in a measured quantity which are known reliably plus one additional digit that is uncertain.
For counting of the significant figure rule are as:
(i) All non- zero digits are significant figure.
(ii) All zero between two non-zero digits are significant figure.
(iii) All zeros to the right of a non-zero digit but to the left of an understood decimal point are not significant. But such zeros are significant if they come from a measurement.
(iv) All zeros to the right of a non-zero digit but to the left of a decimal point are significant.
(v) All zeros to the right of a decimal point are significant.
(vi) All zeros to the right of a decimal point but to the left of a non-zero digit are not significant. Single zero conventionally placed to the left of the decimal point is not significant.
(vii) The number of significant figures does not depend on the system of units.
Addition or subtraction with significatn figure :-
In addition or subtraction , the result should be reported to the same number of decimal places as that of the number with minimum number of decimal places.
For ex: A= 334.5 kg; B= 23.45Kg then A + B =334.5 kg + 23.43 kg = 357.93 kg
The result with significant figures is 357.9 kg
Mutiplication and division in significant figure :-
In multiplication or division, the result should be reported to the same number of significant figures as that of the number with minimum of significant figures.
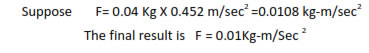
Accuracy in measurement
Accuracy refers to the closeness of a measurement to the true value of the physical quantity and precision refers to the resolution or the limit to which the quantity is measured. The accuracy of a measurement is a measure of how close the measured value is to the true value of the quantity.
Precision
Precision tells us to what limit the quantity is measured.
ROUNDING OFF:
While rounding off measurements the following rules are applied
Rule I: If the digit to be dropped is smaller than 5,then the preceding digit should be left unchanged. For ex: 9.32 is rounded off to 9.3
Rule II: If the digit to be dropped is greater than 5, then the preceding digit should be raised by 1 For ex: 8.27 is rounded off to 8.3
Rule III: If the digit to be dropped is 5 followed by digits other than zero, then the preceding digit should be raised by 1
For ex: 9.351 on being rounded off to first decimal, becomes 9.4
Rule IV: If the digit to be dropped is 5 or 5 followed by zeros, then the preceding digit is not changed if it is even, is raised by 1 if it is odd. For ex:
5.45, on being rounded off,become 5.4
5.450 on being rounded off, becomes 5.4
7.35 , on being rounded off, becomes 7.4
DIMENSIONS, DIMENSIONAL FORMULA AND DIMENSIONAL EQUATION
(1)Dimensions of a derived unit are the powers to which the fundamental units of mass, length
and time etc. must be raised to represent that unit.
![]()
(2)Dimensional formula is an expression which shows how and which of the fundamental units
are required to represent the unit of a physical quantity.M1L1T-2 is the dimensional formula of Force.
CATEGORIES PHYSICAL QUANTITIES
Dimensional Costants: These are the quantities which possess dimensions and have a fixed value.
Ex: Gravitational Constant
Dimensional Variables: These are the quantities which possess dimensions and do not have a fixed value
For ex: velocity, acceleration etc.
Dimensionless Constants: these are the quantities which do not possess dimensions and have a fixed value.
For ex: πetc.
Dimensionless Variables: These are the quantities which are dimensionless and do not have a fixed value.
For ex: Strain, Specific Gravity etc.
Importance of dimentional analysis
A given physical relation is dimensionally correct if the dimensions of the variousterms on either side of the relation are the same.
USES OF DIMENSIONAL EQUATIONS
LIMITATIONS OF DIMENSIONAL ANALYSIS
* It supplies no information about dimensionless constants. They have to be determined either by experiment or by mathematical investigation.
* This method applicable only in the case of power functions. It fails in case of
exponential and trigonometric relations.
* It fails to derive a relation which contains two or more than two quantities of like nature.
* It can only check whether a physical relation is dimensionally correct or not. It cannot tell whether the relation is absolutely correct or not
* It cannot identify all the factors on which the given physical quantity depends upon.





0 Comments