Motion in a Plane Physics Class 11 Physics Formulas Projectile Motion
Scalar Quanties:-
The quantities which have magnitude only but no direction. For example : mass, length, time, speed , temperature etc.
Vector Quantities :-
The quantities which have magnitude as well as direction and obeys vector laws of addition, multiplication etc. For examples : Displacement, velocity, acceleration, force , momentum etc.
Addition of Vectors :-
(i) Only vectors of same nature can be added.
(ii) The addition of two vector A and B is resultant R

Where Θ is the angle between vector A and vector B, And β is the angle which R makes with the direction of A.
(iii) Vector addition is commutative A + B = B+A
(iv) Vector addition is associative,A+ (B +C ) = (A +B )+C
(v) R is maximum if Θ = 0 and minimum if Θ = 180 + 0 .
Subtraction of two vectors :-
(i) Only vector of same nature can be subtracted.
(ii) Subtraction of B from A = vector addition of A and (-B),

Where Θ is the angle between A and B and β is the angle which R makes with the direction of A.
(iii) Vector addition is commutative A + B ≠ B+A
(iv) Vector addition is associative,A+ (B +C ) ≠ (A +B )+C
Rectangular components of a vector in a plane :-
If A makes an angle Θ with x-axis and Ax and By be the rectangular components of A along X-axis and Y- axis respectively.
Then A= A x + By= y
Here A x =A CosΘ and B y = ASinΘ
Dot product or scalar product : -
The dot product of two vectors A and B, represented by . is a scalar , which is equal to the product of the magnitudes of A and B and the Cosine of the smaller angle between them. If Θ is the smaller angle between A and B, then AB= AB

Cross or Vector product :-
The cross product of two vectors and , represented by x is a vector , which is equal to the product of the magnitudes of A and B and the sine of the smaller angle between them. If Θ is the smaller angle between A and B, then = AB Sinθ

Projectile motion : -
Projectile is the name given to anybody which once thrown in to space with some initial velocity, moves thereafter under the influence of gravity alone without being propelled by any engine or fuel. The path followed by a projectile is called its trajectory.

CIRCULAR MOTION
Circular Motion –
When a body moves such that it always remains at a fixed distance from a fixed point then its motion is said to be circular motion. The fixed distance is called the radius of the circular path and the fixed point is called the center of the circular path.
Uniform circular motion:-
When an object follows a circular path at constant speed. The motion of the object is called uniform circular motion.
The magnitude of its acceleration is a c = v2/R.
The direction of a c is always towards the centre of the circle.
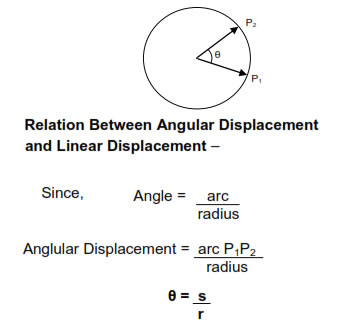
Angular Displacement –
Angle swept by the radius vector of a particle moving on a circular path is known as angular displacement of the particle. Example :– angular displacement of the particle from P1 to P2 is θ.
Angular speed :-
The angular speed is the rate of change of angular distance.
It is related velocity v by V =ω R. The acceleration is ac= ω2R.
If T is the time period of revolution of the object in circular motion and ν is the frequency then we have ω = 2πνV = 2πνR and acceleration a= 4π2 ν 2 R

Instantaneous Angular Velocity –
Angular velocity of a body at some particular instant of time is known as instantaneous angular velocity.
Or
Average angular velocity evaluated for very short duration of time is known as instantaneous angular velocity.

Time Period of Uniform Circular Motion –
Total time taken by the particle performing uniform circular motion to complete one full circular path is known as time period. In one time period total angle rotated by the particle is 2π and time period is T. Hence angular velocity
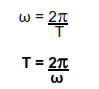
Frequency -
Number of revolutions made by the particle moving on circular path in one second is known as frequency.
f = 1/T = ω/2π
Centripetal Acceleration –
When a body performs uniform circular motion its speed remains constant but velocity continuously changes due to change of direction. Hence a body is continuously accelerated and the acceleration experienced by the body is known as centripetal acceleration (that is the acceleration directed towards the center).
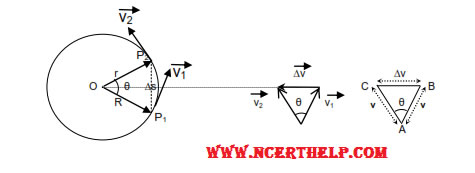
Consider a particle performing uniform circular motion with speed v. When the particle changes its position from P1 to P2. its velocity changes from v1 to v2 due to change of direction. The change in velocity from P1 to p2is ∆v which is directed towards the center of the circular path according to triangle law of subtraction of vectors.
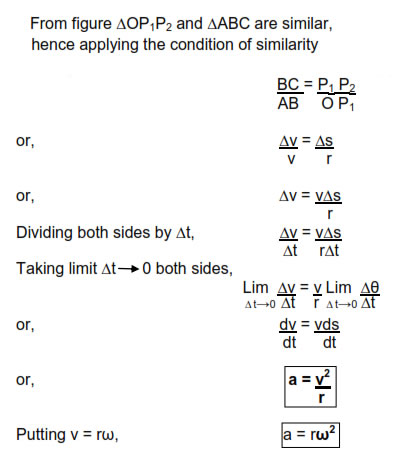
Since the change of velocity is directed towards the center of the circular path, the acceleration responsible for the change in velocity is also directed towards center of circular path and hence it is known as centripetal acceleration.
Centripetal force :-
Centripetal force is the name given to the force that provides inward radial acceleration to a body in circular motion.We should always look for some materia lforce like tension, gravitational force, electrical force, frictionetc. as the centripetal force.
Physical Application of Centripetal Force
i)Case - 1 Circular motion of a stone tied to a string. Centripetal force is provided by the tension of the string
ii) Case - 2 Circular motion of electron around the nucleus. Centripetal force is provided by the electrostatic force of attraction between thepositively charged nucleus and negatively charged electron
iii) Case - 3 Circular motion of planets around sun or satellites around planet. Centripetal force is provided by the gravitational force of attraction between the planet and sun
iv) Case - 4 Circular motion of vehicles on a horizontal road. Centripetal force is provided by the static frictional force between the road and the tyre of the vehicle.
vi) Case - 6 Circular motion of mud particles sticking to the wheels of the vehicle. Centripetal force is provided by the adhesive force of attraction between the mudparticles and the tyres of the vehicle. At very high speed when adhesive force is unable to provide necessary centripetal force, the mud particles fly off tangentially. In order to prevent the particles from staining our clothes, mud-guards are provided over the wheels of vehicle.
vii) Case - 7 Circular motion of a train on a horizontal track. Centripetal force is provided by the horizontal component of the reaction force applied by the outer track on the inner projection of the outer wheels




0 Comments